该比赛已结束，您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。

题目描述

小 A 得到了一张 $n$ 行 $m$ 列的空白大画纸，准备用贴纸来创作一幅画。

小 A 有一张 $c$ 行 $c$ 列的“图案纸”，上面画满了五颜六色的图案。同时，他还有 $k$ 张长方形的透明贴纸。

他会按顺序将这 $k$ 张贴纸依次贴到大画纸上。对于每一张贴纸，我们知道以下信息：

1. 它要贴在画纸上的区域：从左上角格子 $(x_1, y_1)$ 到右下角格子 $(x_2, y_2)$。
2. 它要使用的图案：图案来自于“图案纸”上以 $(x_t, y_t)$ 为左上角的对应区域。也就是说，画纸上的 $(x_1, y_1)$ 格子会被着上图案纸上 $(x_t, y_t)$ 的颜色；画纸上的 $(x_1+1, y_1+2)$ 格子会被着上图案纸上 $(x_t+1, y_t+2)$ 的颜色，以此类推。
3. 它的重要性 $p$：这是一个整数。当两张贴纸覆盖了同一个格子时，重要性数值更大的贴纸会盖在上面。

现在，给你所有贴纸的信息，请问当小 A 把所有贴纸都贴完后，整张大画纸最终是什么样子的？对于没有被任何贴纸覆盖的格子，我们用 $-1$ 来表示。

输入格式

输入共 $k + c + 1$ 行。

第一行，四个整数 $n, m, c, k$，分别代表大画纸的行数和列数、图案纸的边长，以及贴纸的数量。
接下来 $k$ 行，每行七个整数 $x_1, y_1, x_2, y_2, p, x_t, y_t$，描述一张贴纸的信息。它们分别代表：贴在画纸上的左上角行号、列号，右下角行号、列号，贴纸的重要性，以及在图案纸上取图的左上角行号、列号。
接下来 $c$ 行，每行 $c$ 个整数，共同描述了这张 $c \times c$ 的图案纸。

输出格式

输出共 $n$ 行，每行 $m$ 个用空格隔开的整数，代表最终画纸上每个格子的颜色。对于没有被任何贴纸覆盖的格子，输出 $-1$。

输入输出样例 #1

输入 #1

4 4 4 2
1 1 2 2 7 1 1
2 2 3 3 9 3 3
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16

输出 #1

1 2 -1 -1
5 11 12 -1
-1 15 16 -1
-1 -1 -1 -1

说明/提示

样例 1 解释

我们有一张 $4 \times 4$ 的画纸，一张 $4 \times 4$ 的图案纸，和 $2$ 张贴纸。

• 第一张贴纸：重要性为 $7$，要覆盖画纸上 $(1,1)$ 到 $(2,2)$ 的区域，图案取自图案纸的 $(1,1)$ 开始的区域。

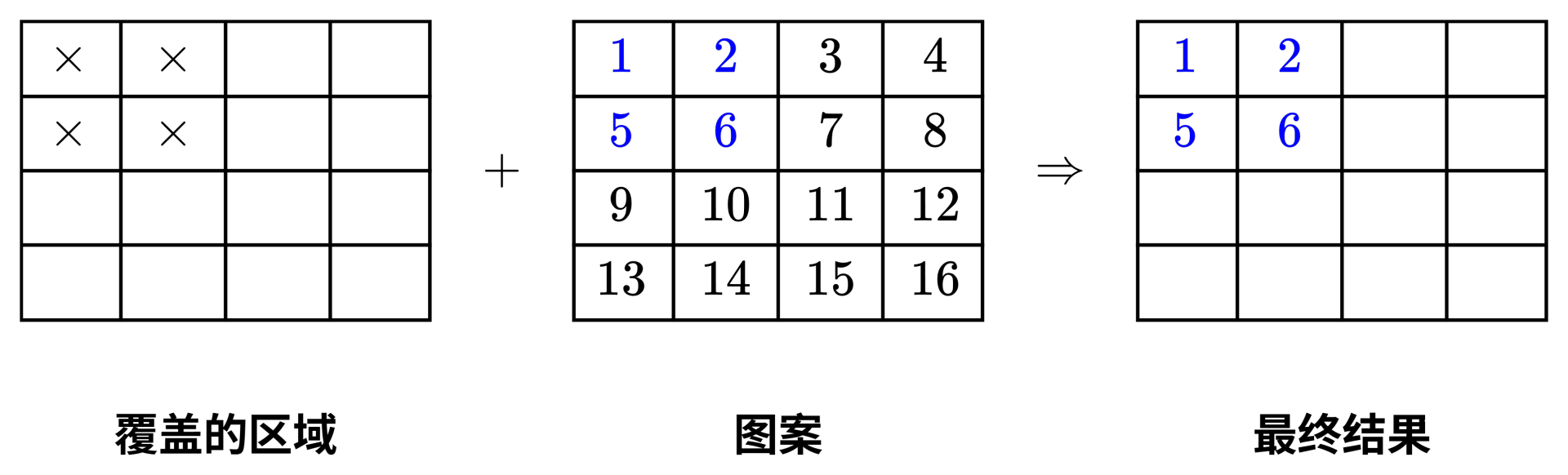
• 第二张贴纸：重要性为 $9$，要覆盖画纸上 $(2,2)$ 到 $(3,3)$ 的区域，图案取自图案纸的 $(3,3)$ 开始的区域。

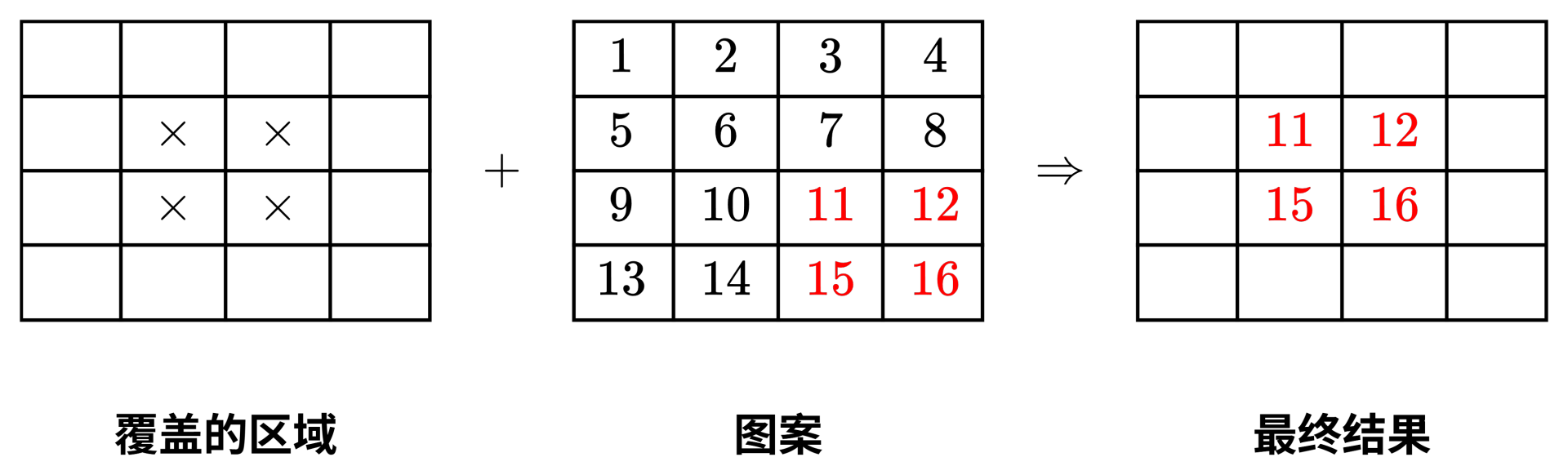
最终，画纸上的 $(2,2)$ 格子被两张贴纸覆盖了。

• 第一张贴纸想把它变成颜色 $6$（重要性为 $7$）。
• 第二张想把它变成颜色 $11$（重要性为 $9$）。

因为 $7 < 9$，所以第二张贴纸更重要，会盖在上面。所以 $(2,2)$ 格子的最终颜色是 $11$。

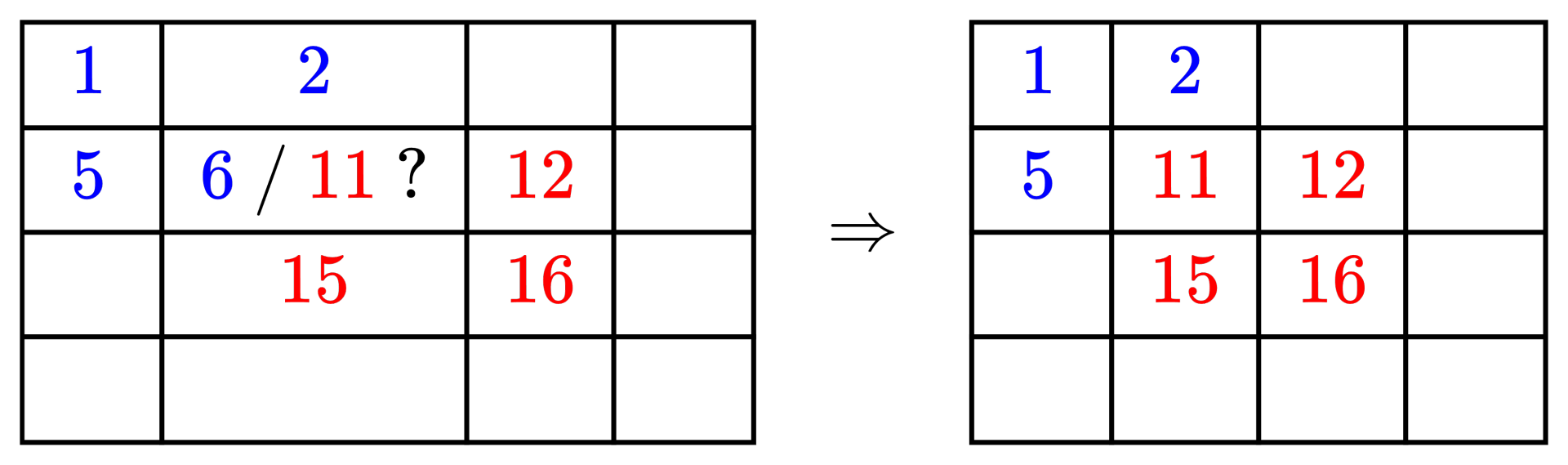
数据规模与约定

本题共 $10$ 个测试点。对于 $100\%$ 的数据：

• $1 \leq n, m, c \leq 500$。
• $1 \leq k \leq 100$。
• 对于每张贴纸，$1 \leq x_1 \leq x_2 \leq n$，$1 \leq y_1 \leq y_2 \leq m$，$1 \leq x_t, y_t \leq c$。
• 保证每张贴纸需要的图案部分，都不会超出图案纸的边界。
• $1 \leq p \leq 10^6$，图案纸中的颜色值范围为 $0 \sim 256$，各贴纸的重要性不同。